Documentation

What is ænet?

The Atomic Energy NETwork (ænet) package is a collection of tools for the construction and application of atomic interaction potentials based on artificial neural networks (ANN). The ænet code allows the accurate interpolation of structural energies, e.g., from electronic structure calculations, using ANNs. ANN potentials generated with ænet can then be used in larger scale atomistic simulations and in situations where extensive sampling is required, e.g., in molecular dynamics or Monte-Carlo simulations.

License

The aenet source code is subject to the terms of the Mozilla Public License, v. 2.0. If a copy of the MPL was not distributed with this file, You can obtain one at http://mozilla.org/MPL/2.0/.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the Mozilla Public License, v. 2.0, for more details.

Installation

Short installation summary

Compile the L-BFGS-B library
- Enter the directory “./lib”
  
  $ cd ./lib
- Adjust the compiler settings in the “Makefile”
- Compile the library with
  
  $ make
The library file liblbfgsb.a, required for compiling ænet, will be created.
Compile the ænet package
- Enter the directory “./src”
  
  $ cd ./src
- Compile the ænet source code with
  
  $ make -f makefiles/Makefile.XXX
  
  where Makefile.XXX is an approproiate Makefile.
  
  To see a list of available Makefiles just type:
  
  $ make
The following executables will be generated in “./bin”:
- generate.x: generate training sets from atomic structure files
- train.x: train new neural network potentials
- predict.x: use existing ANN potentials for energy/force prediction
(Optional) Install the Python interface
- Enter the directory “./python”
  
  $ cd ./python
- Install the Python module with
  
  $ python setup.py install --user
This will set up the Python ænet module for the current user, and it will also install the user scripts aenet-predict.py and aenet-md.py.

Detailed installation instructions

Except for a number of Python scripts, ænet is developed in Fortran 95/2003. Generally, the source code is tested with the free GNU Fortran compiler and the commercial Intel Fortran compiler, and the Makefile settings for these two compilers are provided. While the ænet source code should be platform independent, we mainly target Linux and Unix clusters and ænet has not been tested on other operating systems.

ænet requires three external libraries:

BLAS (Basic Linear Algebra Subprograms),
LAPACK (Linear Algebra PACKage),
And the L-BFGS-B optimization routines by Nocedal et al.

Usually, some implementation of BLAS and LAPACK comes with the operating system or the compiler. If that is not the case, the libraries can be obtained from Netlib.org. libblas.a and liblapack.a have to be in the system library path in order to compile ænet.

The L-BFGS-B routines, an implementation of the bounded limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm, is distributed on the homepage of the authors (Nocedal et al.). For the user’s convenience we have decided to distribute the original L-BFGS-B files along with ænet package, so you do not have to actually download the library yourself. However, each application of ænet should also acknowledge the use of the L-BFGS-B library by citing:

R. H. Byrd, P. Lu and J. Nocedal, SIAM J. Sci. Stat. Comp. 16 (1995) 1190-1208.

ænet’s Python interface further relies on NumPy and on the Atomic simulation Environment, so these dependencies have to available when the ænet Python module is set up.

Compilation of external libraries that are distributed with ænet

All external libraries needed by the ænet code are in the directory “./lib”. Currently, only one external library is distributed with ænet, the L-BFGS-B library (see above).

To compile the external libraries

Enter the directory “./lib”

$ cd ./lib
Adjust the compiler settings in the “Makefile”

The Makefile contains settings for the GNU Fortran compiler (gfortran) and the Intel Fortran compiler (ifort). Uncomment the section that is appropriate for your system.
Compile the library with

$ make

The static library “liblbfgsb.a”, required to build ænet, will be created.

Build ænet

The ænet source code is located in “./src”.

Enter “./src”

$ cd ./src
To see a short explanation of the Makefiles that come with ænet, just run make without any options.

$ make

Select the Makefile that is appropriate for your computer.
Compile with

$ make -f makefiles/Makefile.XXX

where Makefile.XXX is the selected Makefile.

Three executables will be generated and stored in “./bin”:

generate.x: generate training sets from atomic structure files
train.x: train new neural network potentials
predict.x: use existing ANN potentials for energy/force prediction

Set up the Python interface

Enter the directory “./python”

$ cd ./python
Install the Python module with

$ python setup.py install --user

This will set up the Python ænet module for the current user, and it will also install the user scripts aenet-predict.py and aenet-md.py.

General concepts

ænet provides tools for the construction and application of artificial neural network (ANN) potentials. Users who just want to use ænet for simulations based on existing ANN potentials can safely skip over section [[construction] that explains the construction of ANN potentials directly to section simulation.

Potential construction using ænet is broken down into two separate tasks: (i) the compilation of reference structures and energies into a single training set file using the tool generate.x and (ii) the actual fit of the ANN potentials using the tool train.x. The usage of these tools is described in section construction.

Simulations based on existing ANN potentials is enabled by the ænetLib library. ænetLib provides routines for parsing ANN potential files and for energy and force evaluation. Part of the ænet package are sample implementations in Fortran and Python that interface with ænetLib. These tools are discussed in section simulation.

A schematic of the interplay of the different ænet tools is shown in figure flowchart (taken from reference [1]).

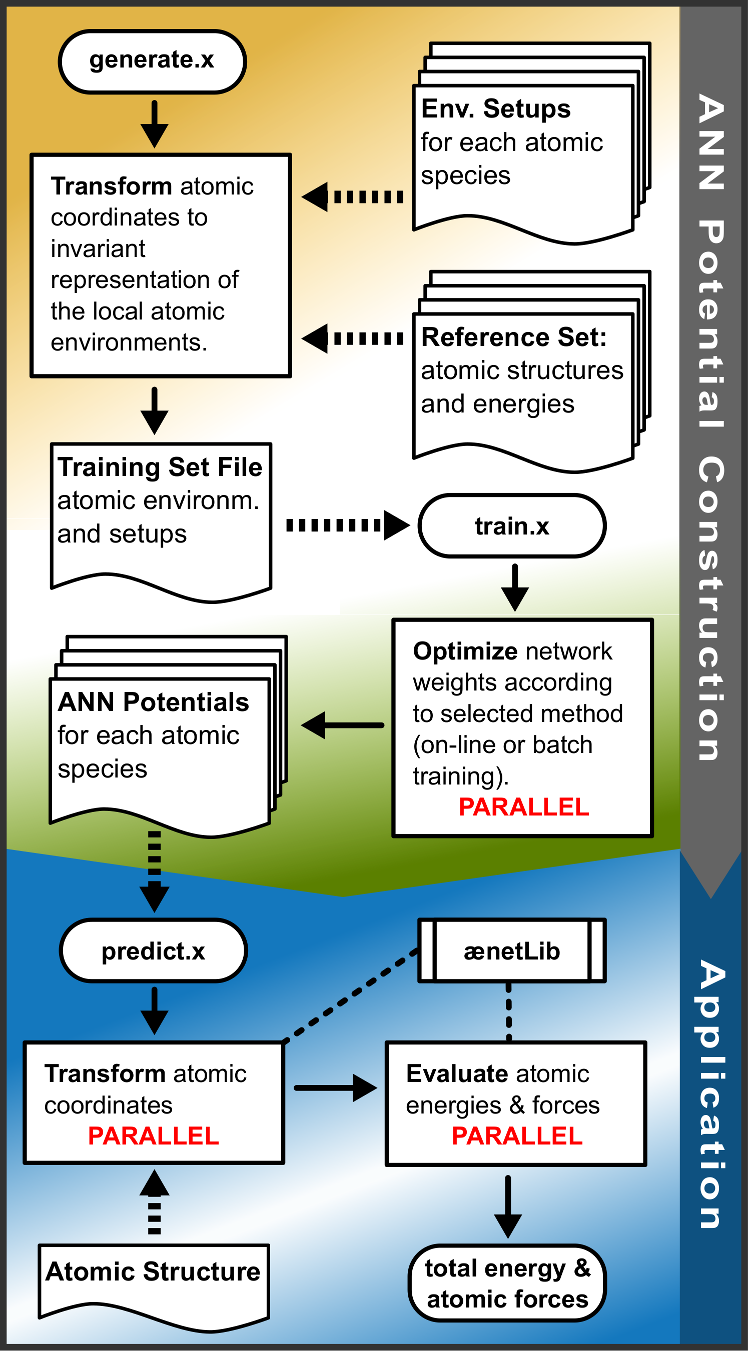
The ænet tools generate.x, train.x, and predict.x are controlled via keyword-based input files. The keywords understood by each of the tools are discussed in their corresponding section; the order in which keywords appear in the input files is arbitrary. Keywords are not case sensitive.

References

Every scientific publication containing results that were produced with ænet should cite the appropriate original references.

The reference for the ænet package itself is: [1] N. Artrith and A. Urban, Comput. Mater. Sci. 114 (2016) 135-150.

If the local structural environment is represented by a Chebyshev descriptor, please cite: [2] N. Artrith, A. Urban, and G. Ceder, Phys. Rev. B 96 (2017) 014112.

The interpolation of atomic energies with ANNs was first published in: [3] J. Behler and M. Parrinello, Phys. Rev. Lett. 98 (2007) 146401.

If the local structural environment is represented by symmetry functions, please cite: [4] J. Behler, J. Chem. Phys. 134 (2011) 074106.

If the SOAP (smooth overlap of atomic positions) descriptor is used for the representation of the local structural environment, please cite: [5] A. P. Bartók, M. C. Payne, R. Kondor, and G. Csányi, Phys. Rev. Lett. 104 (2010) 136403.

The L-BFGS-B method is provided by a third party library. Whenever the method is used for training, please cite: [6] R. H. Byrd, P. Lu and J. Nocedal, SIAM J. Sci. Stat. Comp. 16 (1995) 1190-1208.

The references for the Levenberg-Marquardt method are: [7] K. Levenberg, Q. Appl. Math. 2 (1944) 164–168; [8] D. W. Marquardt, SIAM J. Appl. Math. 11 (1963) 431–441.

ANN potential construction

The construction of a new ANN potential is accomplished by interpolation of structural energies in a reference data set. The structure format used by ænet is explained in section reference-set.

To be useful for general atomistic simulations, ANN potentials have to be invariant with respect to rotation/translation of the structure and exchange of equivalent atoms. Hence, the atomic coordinates have to be represented in a basis that fulfills these conditions. The specification of basis setups (structural fingerprint setups) is topic of section invariant-basis.

The transformation from Cartesian coordinates to invariant coordinates is the purpose of the tool generate.x, which iterates through a list of reference structures and transforms each structure’s coordinates using the method specified in the input file. The input file format for generate.x is discussed in section generate.

Finally, train.x implements different optimization algorithms that can be used for the training of ANN potentials. See section train for the usage of train.x and its input file format.

Structural energy reference data

The atomic structure format used by ænet for this purpose is a subset of the XCrySDen Structure Format (XSF) defined on the XCrySDen homepage. Only the atomic positions of single isolated and periodic structures are parsed by ænet, i.e., ænet does neither support animated XSF files (trajectories) nor scalar fields (volumetric data). Additionally, ænet expects atomic symbols as type specifier, atomic numbers are currently not supported. The structural energy is included in the XSF file as a comment of the form # total energy = XXX, where XXX is the energy value. This has the advantage that the resulting file is still a valid XSF file and can be visualized with XCrySDen and various other visualization programs, such as VMD and VESTA.

Example ænet XSF file of an isolated structure

The following is an example XSF file of an isolated (non-periodic) structure. Each line following the keyword ATOMS contains the atomic symbol, the three Cartesian coordinates, and the three components of the Cartesian force vector. In principle, any unit system may be used, but the length, energy, and force units have to be consistent. The example below uses Å, eV, and eV/Å.

Note that it is advisable to work with a greater number of decimals for the coordinates and atomic forces than used in the example to avoid loss of accuracy.

# total energy = -19543.67017695 eV

ATOMS
O   5.900  3.922  0.851 -0.001  0.001 -0.001
C   5.133  4.445  0.095  0.082  0.104  0.206
O   4.104  5.151  0.087  0.003 -0.001  0.000

Example ænet XSF file of a periodic structure

The following is an example of an XSF file of a periodic structure. The PRIMVEC block contains the lattice vectors in rows. For periodic structures, the number of atoms in the simulation cell has to be specified on the line following the keyword PRIMCOORD (the example is for 6 atoms). Note that the number 1 following the atom count is not relevant for ænet. The same comments as for the isolated structure example above apply.

# total energy = -4990.44928342 eV

CRYSTAL
PRIMVEC
   2.967  0.000  0.000
   0.000  4.648  0.000
   0.000 -0.000  4.648
PRIMCOORD
6 1
Ti 1.483  2.324  2.324  0.000  0.000  0.000
Ti 0.000  0.000  0.000  0.000  0.000  0.000
O  1.483  0.905  0.905  0.000 -0.004 -0.004
O  1.483  3.742  3.742  0.000  0.004  0.004
O  0.000  1.418  3.230  0.000  0.004 -0.004
O  0.000  3.230  1.418  0.000 -0.004  0.004

Invariant basis (structural fingerprint)

Currently, ænet implements two descriptors for the local atomic environment: the Artrith-Urban-Ceder descriptor based on a Chebyshev expansion [2] and the invariant symmetry function basis by Behler and Parrinello [3,4]. The code is designed such that implementing further methods is straightforward.

List of keywords

All keywords are case insensitive, but currently have to occur in the given order. Blank lines and lines starting with !, #, or % are ignored.

descr (optional) Short text that describes the structural fingerprint setup and possible reference citations. Has to be terminated by “end descr”.
atom (required) The chemical species (symbol) of the central atom whose environment is captured by the setup.
env (required) A list of all atomic species that may occur in the environment of the central atom and are captured by this setup. No blank lines are allowed.
rmin (required) The minimal allowed distance between two atoms (in the distance unit used in the XSF files). This value is used by the neighbor list.
basis (required unless functions is present) Definition of a basis set for the expansion of the local atomic environment. Below, an example for the ‘Chebyshev’ basis type is given.
functions (required unless basis is present) Type and parameters of individual basis functions. The example below is for functions of the general type ‘Behler2011’, and the names of the various functions and parameters follows the original publication by Behler. No blank lines allowed.

Input file template using a pre-defined basis set (atomtype.stp)

DESCR
  short desscription and reference
END DESCR

ATOM <atom type>

ENV  <N>
<T_1>
<T_2>
...
<T_N>

RMIN <R>

BASIS type=<basis type>
<basis set parameters>

Input file template using explicit basis function definitions (atomtype.stp)

DESCR
  short desscription and reference
END DESCR

ATOM <atom type>

ENV  <N>
<T_1>
<T_2>
...
<T_N>

RMIN <R>

FUNCTIONS type=<basis type>
<NF>
<parameters of function 1>
<parameters of function 2>
...
<parameters of function NF>

Input file example using a Chebyshev basis set (Ti.fingerprint.stp)

The following example uses a Chebyshev basis set with a cutoff of 8.0 Å for the radial expansion (expansion order 16) and a cutoff of 6.5 Å for the angular expansion (expansion order 4).

DESCR
  Structural fingerprint setup for Ti in bulk TiO2.
  TiO2 reference data set:
    N. Artrith and A. Urban, Comput. Mater. Sci. 114 (2016) 135-150.
  Chebyshev descriptor:
    N. Artrith, A. Urban, and G. Ceder, Phys. Rev. B 96 (2017) 014112.
END DESCR

ATOM Ti

ENV  2
Ti
O

RMIN 0.75d0

BASIS type=Chebyshev
radial_Rc = 8.0  radial_N = 16 angular_Rc = 6.5  angular_N = 4

Input file example using explicit Behler2011 basis functions (Ti.fingerprint.stp)

DESCR
  Structural fingerprint setup for Ti in bulk TiO2.
  Ref.: N. Artrith and A. Urban,
        Comput. Mater. Sci. 114 (2016) 135-150.
END DESCR

ATOM Ti

ENV  2
Ti
O

RMIN 0.75d0

FUNCTIONS type=Behler2011
70
G=2 type2=O   eta=0.003214  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.003214  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.035711  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.035711  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.071421  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.071421  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.124987  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.124987  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.214264  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.214264  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.357106  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.357106  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=0.714213  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=0.714213  Rs=0.0000  Rc=6.5000
G=2 type2=O   eta=1.428426  Rs=0.0000  Rc=6.5000
G=2 type2=Ti  eta=1.428426  Rs=0.0000  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= -1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= 1.0  zeta= 1.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= -1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= 1.0  zeta= 2.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= -1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.000357 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.000357 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.000357 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.028569 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.028569 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.028569 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=O    eta=0.089277 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=O  type3=Ti   eta=0.089277 lambda= 1.0  zeta= 4.0  Rc=6.5000
G=4 type2=Ti type3=Ti   eta=0.089277 lambda= 1.0  zeta= 4.0  Rc=6.5000

Training set generation with `generate.x`

Provided a principle input file and all required structural fingerprint setups, generate.x is run on the command line simply with

$ generate.x generate.in > generate.out

where generate.in is the principal input file, and the output will be written to generate.out. The code will generate a training set file that can be used for the training of ANN potentials.

The format and keywords of the principal input file are described in the following.

Alphabetic list of keywords

All keywords are case insensitive and independent of the order. Blank lines and lines starting with !, #, or % are ignored.

debug (optional) Activate debugging mode; additional output will be generated.
files (required) Specifies number of and path to reference structures in the ænet XSF format. The first line following the keyword contains the number <NF> of structure files. Each of the <NF> following lines contains a file system path.
output (optional) Defines the path to the training set file that is going to be generated. The default name is “refdata.train”. Note that the training set file is in a binary format and cannot be viewed by a text editor. Depending on the number of reference structures, the file can become very large (e.g., 1 GB).
setups (required) Specifies paths to structural fingerprint basis function setup files. Each of the <NT> lines following the keyword contains the chemical symbol <T_i> and the path to the setup file for one species.
timing (optional) Activate timing; additional output files will be created.
types (required) Defines the number of atomic species, their names, and atomic energies. The first line after the keyword contains the number of different species <NT>; the following <NT> lines each contain the chemical symbol <T_i> and atomic energy <E_atom-i> of one species.

Input file template (generate.in)

OUTPUT  <path/to/output/file>

TYPES
<NT>
<T_1>   <E_atom-1>
<T_2>   <E_atom-2>
...
<T_NT>  <E_atom-NT>

SETUPS
<T_1>   <path/to/setup-1>
<T_2>   <path/to/setup-2>
...
<T_NT>  <path/to/setup-NT>

FILES
<NF>
<path/to/file-1.xsf>
<path/to/file-2.xsf>
...
<path/to/file-NF.xsf>

Input file example (generate.in) for TiO₂

The atomic energies defined in the TYPES section is subtracted from the total energy before the potential training to reduce the fluctuations in the fitted energy (the target energy). Two different approaches towards selecting the atomic energies are shown below: In Comput. Mater. Sci. 114 (2016) 135-150 the atomic energies are chosen to be the energies of isolated atoms. With this choice, the trained energy (total energy minus atomic energies) corresponds to the cohesive energy, which is reported by ænet’s predict.x tool.

OUTPUT  TiO2.train

TYPES
2
O   -432.503149303  ! eV
Ti -1604.604515075  ! eV

SETUPS
O   O.fingerprint.stp
Ti Ti.fingerprint.stp

FILES
7815
./structures/0001.xsf
./structures/0002.xsf
...
./structures/7815.xsf

Alternatively, the atomic energies can be set to the average atomic energy of all structures in the reference data set to minimize the range of the target energy (e.g., Phys. Rev. B 96, 2017, 014112). The downside of this approach is that the energy difference is no longer interpretable, i.e., it does not correspond to the cohesive energy.

OUTPUT TiO.train

TYPES
2
O   -433.23448532  | eV
Ti -1626.66972707  | eV

SETUPS
O   O.fingerprint.stp
Ti Ti.fingerprint.stp

FILES
7815
./structures/0001.xsf
./structures/0002.xsf
...
./structures/7815.xsf

ANN potential training with `train.x`

ANN potential training with train.x requires a training set file compiled by generate.x (section generate). A number of optimization methods are implemented by train.x. Apart from the algorithmic differences, the methods differ in their support for parallelization and follow different learning strategies (batch versus online). For a comparison of the different training methods see the ænet implementation reference [1].

train.x expects a principal input file (named “train.in” in the example below). The tool is run from the command line with:

$ train.x train.in > train.out

where the output is written to the file train.out.

The format and keywords of the principal input file are described in the following.

Alphabetic list of keywords

All keywords are case insensitive and independent of the order. Blank lines and lines starting with !, #, or % are ignored.

debug (optional) Activate debugging mode; additional output files will be created.
iterations (optional) Specifies the number of training iterations/epochs (default: 10).
maxenergy (optional) Highest formation energy to include in the training set.
method (optional) Specifies the training method/algorithm to be used for the weight optimization. The line following the keyword contains as first item the name of the method (e.g., bfgs, online_gd, lm) and as further items the parameters of the method (if applicable). The default method is bfgs.
networks (required) Defines the architectures and specifies files for all ANNs. Each of the <NT> (= number of types) lines following the keyword contains the chemical symbol <T_i> of the i-th atomic species in the training set, the path to the ANN output file (binary), and the architecture of the hidden network layers. The latter is defined by the number of hidden layers followed by the number of nodes and the activation function separated by a colon (see example below for two hidden layers of 5 nodes each and the hyperbolic tangent activation).
save_energies (optional) Activate output of the final energies of all training and testing structures. The resulting output files can be used to visualize the quality of the ANN fit and to identify structures that are not well represented. One file per process will be generated, containing only the energies of all structures handled by the process. The files can simply be concatenated.
testpercent (optional) Specifies the percentage of reference structures to be used as independent testing set (default: 10%).
timing (optional) Activate timing; additional output files will be created.
trainingset (required) Defines the name/path to the binary training set file (output of generate.x, e.g., “refdata.train”).

Training methods

The training method is specified with the method keyword followed by the identifier of the method and its parameters. Currently, train.x offers three different optimization methods: online gradient descent, the limited-memory BFGS algorithm and the Levenberg-Marquardt method.

Online gradient descent (online_gd)

Gradient descent is implemented as online learning method which currently prevents efficient parallelization. The method is selected with the identifier online_gd and has two parameters, the learning rate (gamma) that is a measure of the stepsize per iteration, and the momentum parameter (alpha) that controls fluctuations.

An example definition with reasonable parameters is:
```
METHOD
online_gd gamma=3.0d-2 alpha=0.05d0
```
Limited-Memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method

The L-BFGS method is implemented as batch training method, which enables efficient parallelization of the error function evaluation. The method is selected with the identifier bfgs and does not currently offer any adjustable parameters:
```
METHOD
bfgs
```
Levenberg-Marquardt method

The Levenberg-Marquardt method that is presently only available in serial is selected with the identifier lm. The method supports a number of parameters: batchsize sets the number of training points that are used to evaluate the error function at a time. This batch size determines the computational requirements of the method, but should be chosen as large as possible to guarantee convergence. The learnrate is the initial value of the learning rate (see online gradient descent). The parameter iter determines the number of iterations per optimization step used to adjust the learning rate, and the factor used for this adjustment is defined with adjust. Finally, a convergence threshold for the error function can be specified with conv.

Example of reasonable parameters
```
METHOD
lm batchsize=5000 learnrate=0.1d0 iter=3 conv=0.001 adjust=5.0
```

Input file template (train.in)

TRAININGSET <path/to/data/file>
TESTPERCENT <percentage>
ITERATIONS  <NI>
MAXENERGY <emax e.g. -0.05 eV>
SAVE_ENERGIES

METHOD
<method name>  <parameters>

# Examples
#
# (1) online steepest descent
# METHOD
# online_gd gamma=5.0d-7 alpha=0.25d0
# (2) BFGS
# METHOD
# bfgs
# (3) Levenberg-Marquardt
# METHOD
# lm batchsize=1000 learnrate=0.1 iter=1 conv=0.001 adjust=10.0

NETWORKS
# atom   network           hidden
# types  file-name         layers   nodes:activation
<T_1>    <path/to/net-1>     2      5:tanh  5:tanh
<T_2>    <path/to/net-2>     2      5:tanh  5:tanh
...
<T_NT>   <path/to/net-NT>    2      5:tanh  5:tanh

# Example using different activation functions:
# For details see Eq. (1) in:
# N. Artrith and A. Urban, Comput. Mater. Sci. 114 (2016) 135-150.
#
# <T_1>    <path/to/net-1>     2      5:linear  5:linear
# <T_2>    <path/to/net-2>     2      5:linear  5:linear

# <T_1>    <path/to/net-1>     2      5:tanh    5:tanh
# <T_2>    <path/to/net-2>     2      5:tanh    5:tanh

# <T_1>    <path/to/net-1>     2      5:sigmoid 5:sigmoid
# <T_2>    <path/to/net-2>     2      5:twist   5:twist

Example input file (train.in)

TRAININGSET TiO2.train
TESTPERCENT  10
ITERATIONS  500

TIMING

METHOD
lm batchsize=5000 learnrate=0.1d0 iter=3 conv=0.001 adjust=5.0

NETWORKS
! atom   network        hidden
! types  file-name      layers  nodes:activation
  O       O.10t-10t.ann    2    10:twist 10:twist
  Ti     Ti.10t-10t.ann    2    10:twist 10:twist

Restarting training from existing ANN potential

During the training process, ænet creates the restart files train.restart and train.rngstate that contain all information needed to continue the training where it was interrupted. These files will automatically be used when present. If train.x was terminated it might additionally be necessary to copy the most recent ANN weights stored in the final *.ann-XXX files (where XXX is the number of the final training epoch) to corresponding files without epoch number (i.e., simply *.ann).

If no restart is desired, the file train.restart has to be deleted.

Note: Currently, restarting is only implemented for the BFGS training method.

Using ANN potentials for atomistic simulations

It is not the aim of the ænet package to compete with well-established and feature-rich software for molecular dynamics and Monte-Carlo simulations, such as LAMMPS, DL_POLY, TINKER, or ASE. Instead, ænet provides a library with C and Fortran APIs, ænetLib, that can be used to extend existing software by the capability to evaluate ANN potentials constructed with ænet’s train.x. Note that software developed in many other programming languages (e.g., C++, Python, and Java) can interface with C libraries and, hence, is compatible with ænetLib.

A documentation of the ænetLib APIs will be included in a future version of this manual. For the moment, ænet provides two reference implementations for the evaluation of structural energies and forces by linking agains ænetLib: predict.x is written in Fortran and directly uses the Fortran API, and aenet-predict.py, which implements an ASE calculator in Python. In addition, an example Python script for performing simple molecular dynamics simulations with ASE, aenet-md.py, is included in the ænet package.

Prediction of structural energies and atomic forces with `predict.x`

predict.x expects a principal input file (named “predict.in” in the example below) and one or more atomic structure files in the XSF format. The path(s) to the structure files may either be specified in the input file for batch processing, or directly on the command line. The tool is run from the command line with:

$ predict.x predict.in [<structure1.xsf> ...]

All output will be written to standard out.

The format and keywords of the principal input file are described in the following.

Alphabetic list of keywords

All keywords are case insensitive and independent of the order. Blank lines and lines starting with !, #, or % are ignored.

debug (optional) Activate debugging mode; additional output files will be created.
files (optional) Specifies a list of paths to input structures. This keyword may be used for batch processing of a larger number of structures. The line following the keyword contains the number of input files <NF>, and each of the following <NF> lines contains a single file system path. Alternatively, a single input structure may be passed to predict.x as command line argument. The command line takes precedence over the list specified with the “files” keyword.
forces (optional) Activates evaluation of the atomic forces. Forces are also calculated, when the “relax” keyword is present.
networks (required) Specifies the ANN potential files for each chemical species. On each of the <NT> lines following the keyword a chemical species <T_i> and the path to its corresponding ANN file is given.
relax (optional) Activate structural relaxation; this will automatically also activate the calculation of the atomic forces. On the line following the relax keyword, several options can be specified. See the example below.
timing (optional) Activate timing; additional output files will be created.
types (required) Specifies the number of different atomic species that may occur in structures and their chemical symbols. The first line following the keyword specifies the number <NT> of different atom types; the following lines each contain one chemical symbol <T_i>.

Input file template (predict.in)

TYPES
<NT>
<T_1>
<T_2>
...
<T_NT>

NETWORKS
<T_1>  <path/to/NN-1>
<T_2>  <path/to/NN-2>
...
<T_NT> <path/to/NN-NT>

FORCES

# or optimize coordinates:
#
# RELAX
# method=bfgs  F_conv=1.0d-2  E_conv=1.0d-6  steps=99
#
#    method: optimization method (currently only BFGS)
#    F_conv: convergence thershold for the forces
#    E_conv: convergence threshold for the energy
#    steps:  max. number of iterations

FILES
<NF>
<path/to/structure-1.xsf>
<path/to/structure-2.xsf>
...
<path/to/structure-NF.xsf>

Input file example (predict.in) for TiO₂

TYPES
2
Ti
O

NETWORKS
  Ti Ti.10tw-10tw.ann
  O  O.10tw-10tw.ann

FORCES

FILES
10
structure0001.xsf
structure0002.xsf
structure0003.xsf
structure0004.xsf
structure0005.xsf
structure0006.xsf
structure0007.xsf
structure0008.xsf
structure0009.xsf
structure0010.xsf

ASE Interface: `aenet-predict.py` and `aenet-md.py`

The Atomic Simulation Environment (ASE) is a Python framework for atomistic simulations and for the manipulation of atomic structures. ASE provides a simple API, calculators, for interfacing with third-party software for the evaluation of structural energies and atomic forces. The ænet package includes an implementation of an ASE calculator linked to ænetLib. The script aenet-predict.py uses this calculator to essentially replicate the features of predict.x (see above), and aenet-md.py provides simple molecular dynamics capabilities.

The input files for both Python scripts use the JSON format and are compatible. Any structure format supported by ASE can be used as input, however, as of writing, the support of the XSF structure format in ASE is incomplete and other formats (e.g., VASP’s POSCAR format, FHI-aims geometry.in format, XYZ, etc.) are recommended.

Alphabetic list of keywords

The input files of aenet-predict.py and aenet-md.py both use the JSON format. Keywords that are specific to one tool are ignored by the other.

potentials (required) Specifies the ANN potentials for all atomic species.
structure_file (MD only) Path to the file with the initial structure. Every structure format that is understood by ASE can be used.
trajectory_file (MD only) Path to the trajectory file (in ASE’s format) to be generated during the MD simulation.
temperature (MD only) Temperatur for MD simulations in the canonical ensemble.
md_steps (MD only) Number of MD steps.
print_steps (MD only) Number of MD steps between writing output.
time_step (MD only) MD time step in femtoseconds.

Input file template (input.json)

{
    "potentials" : {
        <T1> : <potential1>,
        <T2> : <potential2>,
        ...
    },
    "structure_file" : <initial-structure>,
    "trajectory_file" : <output-file>,
    "temperature" : <T>,
    "md_steps"    : <N_MD>,
    "time_step"   : <dt>,
    "print_steps" : <N_print>
}

Input file example (input.json)

{
    "potentials" : {
        "Ti" : "Ti.10t-10t.ann",
        "O"  : "O.10t-10t.ann"
    },
    "structure_file" : "input.vasp",
    "trajectory_file" : "md.traj",
    "temperature" : 300.0,
    "md_steps"    : 100,
    "time_step"   : 1.0,
    "print_steps" : 1
}

Acknowledgments

This work has been using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575. Since 2019 ænet development has used resources of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. Development has also been supported by the Department of Chemical Engineering at Columbia University.

Questions?

If you run into problems with ænet or if you have a general question, please contact Dr. Nongnuch Artrith (nartrith@atomistic.net).

Bibliography

[1] N. Artrith and A. Urban, Comput. Mater. Sci. 114 (2016) 135-150.

[2] N. Artrith, A. Urban, and G. Ceder, Phys. Rev. B 96 (2017) 014112.

[3] J. Behler and M. Parrinello, Phys. Rev. Lett. 98 (2007) 146401.

[4] J. Behler, J. Chem. Phys. 134 (2011) 074106.

[5] A. P. Bartók, M. C. Payne, R. Kondor, and G. Csányi, Phys. Rev. Lett. 104 (2010) 136403.

[6] R. H. Byrd, P. Lu and J. Nocedal, SIAM J. Sci. Stat. Comp. 16 (1995) 1190-1208.

[7] K. Levenberg, Q. Appl. Math. 2 (1944) 164–168.

[8] D. W. Marquardt, SIAM J. Appl. Math. 11 (1963) 431–441.

Documentation

What is ænet?

License

Installation

Short installation summary

Detailed installation instructions

Compilation of external libraries that are distributed with ænet

Build ænet

Set up the Python interface

General concepts

References

ANN potential construction

Structural energy reference data

Example ænet XSF file of an isolated structure

Example ænet XSF file of a periodic structure

Invariant basis (structural fingerprint)

List of keywords

Input file template using a pre-defined basis set (atomtype.stp)

Input file template using explicit basis function definitions (atomtype.stp)

Input file example using a Chebyshev basis set (Ti.fingerprint.stp)

Input file example using explicit Behler2011 basis functions (Ti.fingerprint.stp)

Training set generation with generate.x

Alphabetic list of keywords

Input file template (generate.in)

Input file example (generate.in) for TiO2

ANN potential training with train.x

Alphabetic list of keywords

Training methods

Input file template (train.in)

Example input file (train.in)

Restarting training from existing ANN potential

Using ANN potentials for atomistic simulations

Prediction of structural energies and atomic forces with predict.x

Alphabetic list of keywords

Input file template (predict.in)

Input file example (predict.in) for TiO2

ASE Interface: aenet-predict.py and aenet-md.py

Alphabetic list of keywords

Input file template (input.json)

Input file example (input.json)

Acknowledgments

Questions?

Bibliography

Table of Contents

Training set generation with `generate.x`

Input file example (generate.in) for TiO₂

ANN potential training with `train.x`

Prediction of structural energies and atomic forces with `predict.x`

Input file example (predict.in) for TiO₂

ASE Interface: `aenet-predict.py` and `aenet-md.py`